There are many 3D coordinate systems, they differ due to their varied etymologies in mathematics, navigation, computer graphics etc. The one used internally by Panaudia is that most commonly used by ambisonics, which were developed by Michael Gerzon and others at Oxford in the early 1970s, and is very similar to the conventions used in avionics.
Positions are represented by x, y and z values in a right-handed, three-dimensional cartesian space with these axes.
- x - positive axis points forwards
- y - positive axis points to the left
- z - positive axis points upwards
Panaudia's Spaces are cubes with a unit size of 1.0. This means that all x, y and z coordinates must be scaled to be between 0.0 and 1.0.
Rotations are represented by yaw, pitch and roll values in degrees:
- yaw - The direction in the horizontal plane, given as an anti-clockwise rotation measured from the positive x=axis in degrees. (- 180 to + 180)
- pitch - The elevation above or below the horizon, given as a positive value for degrees upwards, above the horizon, and negative for below. (- 90 to + 90)
- roll - The tilt to one side or the other, given as an anti-clockwise rotation around the line of sight in degrees. (- 180 to + 180)
This looks something like this:
Ambisonic coordinate system
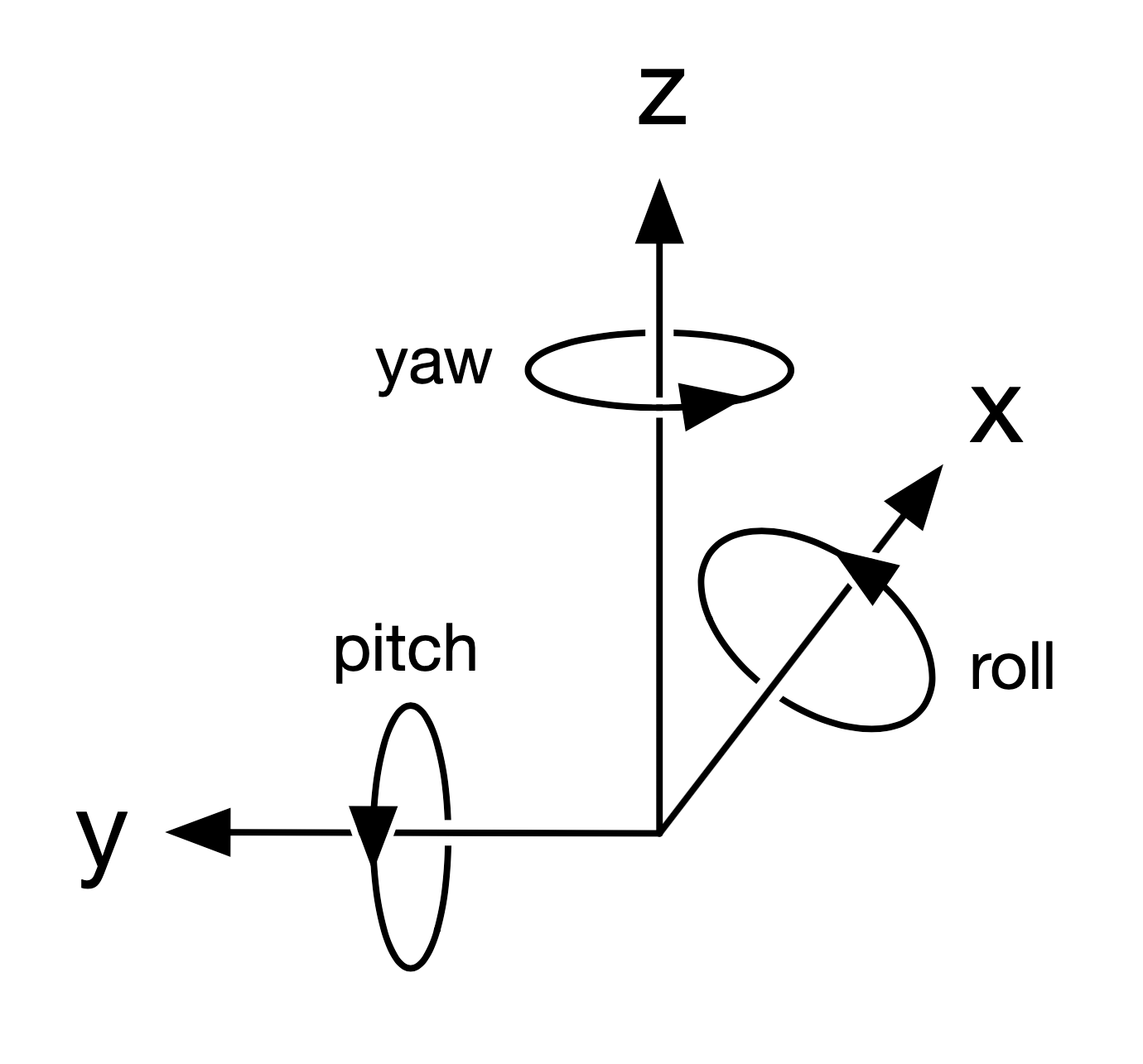
The Panaudia version of this system can be described as:
- Right-Handed Cartesian.
- z up and x forward.
- Bounds (0, 0, 0) to (1, 1, 1).
- Angles in degrees.
- Intrinsic Tait–Bryan rotations in the order yaw-pitch-roll.
You can find a detailed explanation of Euler and Tait–Bryan conventions and difference between intrinsic and extrinsic rotations here https://en.wikipedia.org/wiki/Euler_angles
Coordinates in JavaScript SDK
Another common coordinates system is that used in computer graphics. Probably originating in IRIS GL at Silicone Graphics in the early 1980s this system placed the two principle axes, x and y, on an upright plane, to match the computer screen rather than on the ground. This standard is now the default 3D in web graphics built on WebGL/OpenGL.
OpenGL itself uses extrinsic rotations but most JavaScript libraries like Three.js or React-three-fiber wrap these up in more intuitive intrinsic rotations resulting in a coordinate system that looks like this:
Web 3D coordinate system
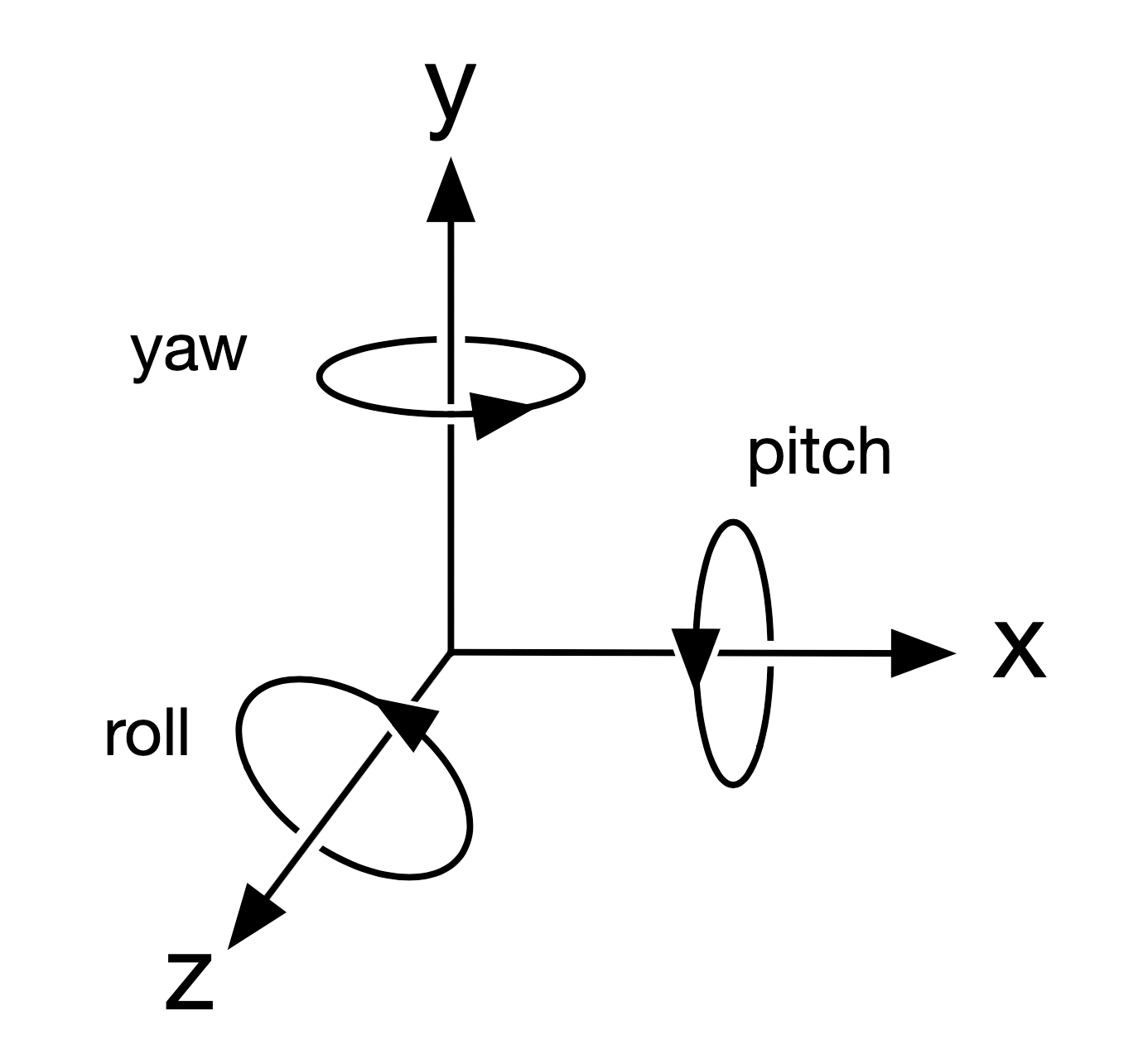
- Right-Handed Cartesian - the same as ambisonics.
- y is up instead of z and -z is forward.
- Bounds (-1, -1, -1) to (1, 1, 1) with the origin at the centre.
- Angles in radians.
- Also uses intrinsic Tait–Bryan rotations but with a different order: pitch-yaw-roll.
As our JavaScript SDK is most likely to be used with this coordinate system we have included automatic conversion between web 3D and ambisonic coordinate systems. These functions will automatically do the conversions for you, their details are here:
A spatial mnemonic for ambisonic coordinates
Ambisonic coordinates, WebGL coordinates and geospatial coordinates are all right-handed cartesian coordinate systems. This is a spatial mnemonic I use to help me quickly remember their relationships to each other.
Imagine you are sitting looking East with your phone flat on the floor in front of you, with its screen facing up and the top of the phone pointing to your left.
Now the x, y and z axes for your head's ambisonic sound field, your geospatial pose and your phone's WebGL renderer are all aligned.
Further reading
These give some extra background information:
- Ambisonics https://en.wikipedia.org/wiki/Ambisonics
- Euler Angles https://en.wikipedia.org/wiki/Euler_angles
- OpenGL Coordinates https://learnopengl.com/Getting-started/Coordinate-Systems